ARTE Y MATEMÁTICAS POR SU AUTOR LYNN GAMWELL
Cuando era un estudiante de doctorado en historia del arte, he leído muchas explicaciones del arte abstracto, pero eran siempre inadecuadas y engañosas. Así que después de terminar mi doctorado, fui a conocer la historia de la biología, la física y la astronomía, y la publicación de un libro que detalla cómo el arte moderno es una expresión de la visión científica del mundo .
Sin embargo, muchas obras de arte también expresan las matemáticas y la tecnología de su época. A la investigación matemática y arte que tenía que aprender conceptos matemáticos como el cálculo, la teoría de grupos y la lógica de predicados. Como un novato tratando de entender estas ideas, me llamó la atención con la mala calidad y el contenido confuso de las ilustraciones en la mayoría de los libros educativos. Por lo tanto, juré crear para mi libro un conjunto de diagramas de matemáticas que son convincentes visualizaciones cristalinas de los conceptos abstractos.
Como profesor de la School of Visual Arts de Manhattan, escribí este libro para mis alumnos, como María, que me dijo que nunca fue bueno en la historia porque no podía recordar fechas, y para Jin Sug, quien falló preparatoria álgebra porque no era capaz de memorizar fórmulas. Espero que van a leer este libro y descubrir que la historia es un libro de cuentos y que la matemática es cautivador sobre las ideas.
Aquí hay diez imágenes seguidas por las descripciones:
A lo largo de la historia, los científicos han descubierto patrones matemáticos en la naturaleza, como los caminos tomados por los electrones a medida que fluyen a través de las colinas y valles de diminutas "paisajes" que se miden en micras (una micra es igual a una millonésima parte de un metro). Trayectorias de los electrones en esta impresión digital se registraron por Eric J. Heller, que estudia las olas gigantes (olas gigantes, olas asesinas) en pequeña y gran escala. Cuando una onda de electrones fluye a través de un ordenador, una ola gigante en un semiconductor puede amenazar repentinamente el buen funcionamiento del dispositivo.
matemática occidental procede mediante el aumento de la abstracción y generalización. En el Renacimiento el arquitecto italiano Filippo Brunelleschi inventó la perspectiva lineal, un método para proyectar objetos geométricos en un "plano del cuadro" de un punto de vista determinado. Tres siglos más tarde, el matemático francés Jean-Victor Poncelet generalizarse en perspectiva de la geometría proyectiva para aviones que se inclinan o giran. Luego, a principios del siglo XX, el holandés LEJ Brouwer generaliza la geometría proyectiva de Poncelet a las proyecciones sobre las superficies que se amplía o reduce en cualquier forma, también llamadas de caucho de la ficha técnica proporciona la geometría que el avión sigue siendo continua (sin agujeros o desgarros), que es el objeto de esta fotografía. El artista contemporáneo Jim Sanborn lo creó mediante la proyección de un patrón de círculos concéntricos en una gran formación rocosa en la noche de alrededor de 1/2 milla de distancia. A continuación, tomó esta fotografía con una exposición larga al salir la luna.
El conocimiento de las matemáticas griegas antiguas, como Euclides y Ptolomeo, se perdió en el Occidente medieval, pero los eruditos islámicos conserva sus escritos en traducciones árabes. En el siglo IX, califas establecieron la Casa de la Sabiduría en Bagdad como un lugar para los estudiosos de adquirir y traducir textos extranjeros en las matemáticas y la filosofía. El trabajo de trece volúmenes de Ptolomeo se conoce hoy con el nombre se lo dieron, Almagesto (en árabe significa "el más grande").
Dos matemáticos contemporáneos, Reza Sarhangi y Robert Fathauer, rendir homenaje al matemático islámico Abu'l-Wafa (AD 940¬-98), que trabajaba en la casa de la sabiduría, donde escribió un texto práctico, sobre las partes de la geometría que necesitan los artesanos . Mostró cómo construir un heptágono regular (un polígono con siete lados y ángulos iguales), que está en la parte central de esta impresión. En todo el perímetro de la heptágono Sarhangi y Fathauer escribió el nombre de Buzjani siete veces en farsi, el idioma de Persia (actual Irán).
Con el desarrollo de los ferrocarriles en el siglo XIX, el tema de la búsqueda de una ruta óptima para un viaje era de interés práctico. El tema entró en la literatura matemática en 1930, cuando el matemático vienés Karl Menger describió como el "problema mensajero" ( das Botenproblem ) de encontrar una vía de administración óptima. Pronto fue apodado "el problema del viajante de comercio" del: dada una lista de las ciudades y las distancias entre cada par, encontrar la ruta más corta que la visita cada ciudad una vez y vuelve a la ciudad de origen
El matemático estadounidense Robert Bosch llegó a esta línea continua sobre la base de la solución a un caso de 5000 de la ciudad del problema del viajante de comercio. Desde la distancia, la impresión parece representar un cordón negro sobre un fondo gris en forma de un nudo celta. Sin embargo, en la inspección cercana de la aparente "gris" es en realidad una línea blanca continua moviéndose en la parte superior de un fondo negro. La línea blanca nunca se cruza a sí mismo, se trata de una red en lugar de un nudo y lo que la respuesta a la punny título es "No".
En 1905, Albert Einstein descubrió la simetría de la masa y la energía-masa se puede convertir en energía, y viceversa (E = mc2). Luego, en las primeras décadas del siglo XX, los físicos y matemáticos, entre ellos Einstein, se reunieron en Zurich y emplea la teoría de grupos en su exploración de la simetría de la naturaleza.
artistas suizos como Gerstner crean patrones que resuenan con estas descripciones matemáticas de la naturaleza en términos de simetría. Al igual que los matemáticos, estos artistas establecieron estéticas bloques de construcción básicos de unidades de color y forma, y los dispuso el uso de normas que preserven la proporción y el equilibrio.
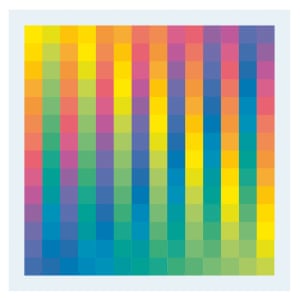
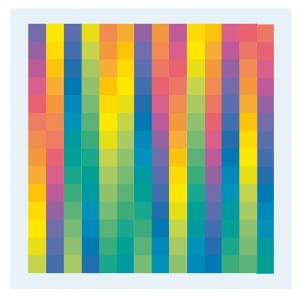
En 1956 Gerstner ideó un sistema de una paleta móvil modular con 196 tonos en 28 grupos-para experimentar con progresiones de forma que enlazan con el color.paleta de 196 plazas de Gerstner tiene 28 grupos con 7 plazas cada uno. Se muestran aquí cuatro de los arreglos miríada de posibles, que el artista describe el uso de términos del matemático: grupos, permutaciones, algoritmos, y la invariancia.
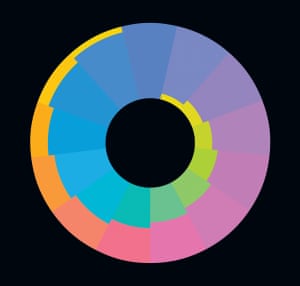
conocimientos científicos en los niveles más profundos del mundo natural son explicaciones basadas en la simetría, que el artista Karl Gerstner simboliza con este "icono" circular para la era secular de la ciencia y la tecnología. La forma geométrica más simétrica es una esfera (todos los puntos equidistantes de un punto en el espacio tridimensional). A finales del siglo XX, los científicos llegaron a la conclusión de que el universo comenzó en perfecta simetría como un punto que explotó en una esfera de plasma. A medida que el universo se expandió para lactantes, se enfrió la esfera primordial, y la materia condensada a partir del plasma para formar las primeras partículas, átomos, entonces las nubes de gas y las estrellas. En algún momento se rompió la simetría original del universo; las asimetrías resultantes parecen ser el resultado de cambios aleatorios análogos a mutaciones durante la evolución. Hoy en día, los físicos están recreando muestras de este plasma esférica primordial para determinar el grado en el cual el universo se conserva rastros de su simetría inicial.
Simon Thomas es un joven artista británico cuyo trabajo, como esta escultura, es una visualización de una fórmula matemática. Estudió artes visuales en el Royal College of Art en Londres en la década de 1980 y llegó a crear la escultura con sorprendentes patrones geométricos, que actúa como artista en residencia en la Universidad de Bristol, tanto en el departamento de la física (1993-1995) y matemáticas (2002).
......................
Este es un puesto de invitado en el blog de Alex Bellos matemáticas. El libro más reciente de Alex es un libro para colorear matemático, llamado copo de nieve de la estrella del Seashell en el Reino Unido y los patrones del Universo en los EE.UU..
www.theguardian.com







con el tiempo. Wölfflin identificó cinco transformaciones - por ejemplo, de lineal a pictórico - para describir los cambios de estilo del Renacimiento al Barroco. En la Universidad de Zurich, donde enseñó Wölfflin, su colega Speiser de la Facultad de Física asistió regularmente a sus clases. Speiser hubiera gustado ver una visualización de una transformación en virtud de la invariancia, donde el mismo sujeto (como un retrato), pintado en un estilo lineal durante el Renacimiento, es transformada por un artista usando un estilo pictórico en el Barroco.observer.com
ResponderEliminarLas raíces históricas de la teoría de grupos son la teoría de las ecuaciones algebraicas, la teoría de números y la geometría. Euler, Gauss, Lagrange, Abel y Galois fueron los creadores que ponen los cimientos de esta rama del álgebra abstracta. Évariste Galois es reconocido como el primer matemático que relacionó esta teoría con la teoría de cuerpos, de lo que surgió la teoría de Galois. Además, usó la denominación de grupo o " inventó el término [...]" según E.T.Bell. Otros importantes matemáticos que contribuyen son Cayley, Emil Artin, Emmy Noether, Peter Ludwig Mejdell Sylow, A.G. Kurosch, Iwasawa entre muchos otros. Fue Walter Dick quien en 1882, dio la moderna definición de grupo y fue "el primero en definir el grupo libre engendrado por un número finito de generadores", según Nicolás Bourbaki. A fines del siglo XIX, Frobenius definió grupo abstracto con un sistema de axiomas.
ResponderEliminares.wikipedia.org
Los científicos confirmaron además que las leyes de la naturaleza, como la fuerza de gravedad y la velocidad de la luz, son simétricas en el sentido de que se aplican por igual en todo el Universo. Estos descubrimientos han encontrado una amplia aplicación, incluso inspirando a algunos artistas para crear expresiones icónicas de la simetría de la naturaleza en su arte. Habían aprendido de la cosmología de Einstein de popularizaciones como propia de Einstein de la relatividad: La teoría especial y general, una exposición popular (1917). Karl Gerstner, un joven artista en la década de 1950 y un líder de este nuevo movimiento, expresó la imposibilidad de un solo punto de vista humano en la obra Aperspective : 12 unidades de color blanco y negro fijados a los imanes, los cuales pueden cambiar de posición sin fin dentro de un marco fijo - al igual que la luz se mueve a través del cosmos de Einstein como un infinito acotado.
ResponderEliminarEl trabajo de Gerstner está en la tradición del arte concreto suizo, que fue fundada en Zurich en la década de 1930 y 40 de Max Bill, Camille Graeser, Richard Paul Lohse y Verena Loewensberg. Zurich era un lugar donde los físicos y matemáticos, entre ellos Einstein, Andreas Speiser y Hermann Weyl, se reunieron para dar una descripción unificada de las fuerzas de la naturaleza: la gravedad, el electromagnetismo, la fuerza nuclear fuerte y la fuerza nuclear débil. Ellos usan las matemáticas de la teoría de grupos para describir la simetría, que es la propiedad de permanecer sin cambios cuando ciertas operaciones se llevan a cabo. Por ejemplo, imagina dibujar una línea en el centro de una persona de pies a cabeza, dividiendo el cuerpo en los lados izquierdo y derecho. Si la persona hace un giro de la mitad (180 grados) y luego una vuelta completa (360 grados), la silueta del cuerpo no cambia en estas dos posiciones, ya que ha dejado a la derecha-(o "espejo") simetría. En el lenguaje de la teoría de grupos, el cuerpo se doble simetría de rotación alrededor de un eje.
Karl Gerstner, Aperspective 1: La espiral sin fin de un ángulo recto, 1952-1956. pinturas de resina sintética en los paneles de plexiglás 12, 3 ½ x 17 ¾ pulg. (9 × 45 cm) ea., se sujeta con imanes á hierro sobre una base de plexiglás negro, 39 3/8 x 39 3/8 pulg. (100 × 100 cm). Cortesía del artista.
Inspirado por popularizaciones de la teoría de grupos Speiser y de Weyl, artistas concretos suizos crearon obras con simetría sorprendente mediante el establecimiento de bloques de construcción básicos estéticos - unidades de forma y color - y la organización de ellos usando reglas que preservan la proporción y el equilibrio. Por ejemplo, los bloques de construcción de Gerstner de azul Excentrum son círculos, líneas, azul, negro, y blanco, a los que se aplican las reglas: el doble de la dimensión de cada círculo con incrustaciones y el color de la luz de color azul oscuro; trazar una línea vertical en el perímetro de cada círculo y colorear cada "rebanada" del blanco al negro.
Psicólogos alemanes de principios del siglo 20 encontraron pruebas de que el ojo humano, oído y el cerebro tienen mecanismos innatos para percibir un patrón, llamado Gestalt (alemán para "forma" o "forma"), así como una capacidad de distinguir los patrones simétricos. El uso de estos conceptos, el historiador de arte suizo Heinrich Wölfflin explicó cómo los espectadores perciben el arte, la incorporación de las ideas de la teoría de grupos para describir cómo los estilos artísticos cambian con el tiempo.
observer.com en este blog