ENIGMAS POR EL DÍA DE Pi
El día de hoy que se establece el siguiente enigma:
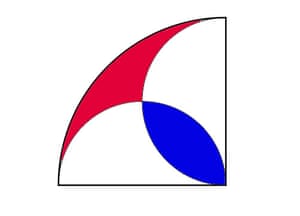
a continuación se ilustra es un cuarto de círculo, que contiene dos semicírculos de círculos más pequeños. Demostrar que el segmento de color rojo tiene la misma área que el azul.
Solución
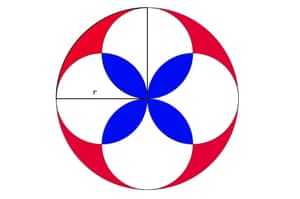
Coloque cuatro cuartos de círculo idénticas entre sí para ver el círculo completo.Podemos ver que se compone de cuatro círculos más pequeños que se superponen.
De su análisis de las áreas en el diagrama podemos deducir lo siguiente:
- El área de los cuatro círculos más pequeños superpuestos (las secciones blancas y azul) es igual al área de cuatro de estos círculos menos el área del solapamiento (la sección azul).
- El área de todo el círculo menos el área de la sección roja es igual al área del blanco y las secciones azules.
Es Pi Day! Te dije que el área de un círculo es pi veces el radio al cuadrado. Por lo que el área del círculo grande es π r 2 .
El radio de cada uno de los círculos más pequeños es media r, o r / 2. Así el área de cada círculo más pequeño es π ( r / 2) 2 , o π r 2 / 2 2 , que es π r 2 / 4.
Por lo tanto, el área de los cuatro círculos más pequeños es de 4 x π r 2 / 4 = π r 2 .
Ahora podemos reformular las dos instrucciones por encima de la siguiente manera:
- La sección blanca y azul es igual a π r 2 de la sección azul menos.
- La sección blanca y azul es igual a π r 2 de la sección roja de menos.
Si estas declaraciones son verdaderas, las secciones azules y rojas deben ser iguales. Debido a que cada trimestre tiene la misma proporción de azul a rojo, azul cada sección debe tener la misma zona que cada uno rojo.
Este puzzle aparece en el Tokyo Rompecabezas por Kobon Fujimura.
Me publicar un rompecabezas aquí cada segundo lunes. Mi libro más reciente es la matemática de libro para colorear de adultos del copo de nieve estrella del Seashell .(En los EE.UU. su título es Patrones del Universo .)
Usted puede comprobar fuera de mí en Twitter , Facebook , Google+ y mi página web personal . Y si sabemos de ningún gran rompecabezas que le gustaría que fije aquí,ponerse en contacto .
www.theguardian.com

¿Qué es la topología? ¿Es como la geometría?
ResponderEliminarLa geometría es específica y la topología es general. Los topólogos estudian grandes rasgos y categorías de formas. Por ejemplo, en geometría un cubo y una esfera son diferentes. Pero en topología son iguales (o equivalentes) porque puedes transformar el uno en el otro sin cortar sus superficies. El toro, una esfera con un agujero en el medio, es una forma diferente. Es claramente diferente de una esfera porque no puedes transformar un toro en una esfera de ninguna manera.
¿Significa eso que la geometría y la topología son dos perspectivas de la misma cosa?
Sí. Es como la literatura china. Un poema podría describir una despedida entre amantes. Pero en el lenguaje del poema, en vez de un hombre y una mujer, hay un sauce, cuyas hojas son suaves y están colgando. El modo en que la rama cuelga es como el sentimiento del hombre y de la mujer queriendo estar juntos. La geometría nos da una estructura del sauce que es sólida y extensiva. La topología describe la forma global del árbol sin los detalles – pero sin el árbol, no tendríamos nada.
Siempre me ha asombrado observar cómo diferentes grupos de personas miran una misma cosa. Mis amigos físicos miran al espacio-tiempo desde la perspectiva de la física real, pero la teoría de la relatividad describe el espacio-tiempo en términos de geometría, porque así es como Einstein miró al problema.
Cuando miró al mundo a través de la lente de la geometría y la topología, ¿qué aprendió?
Que las ecuaciones no lineales eran fundamentales porque en la naturaleza, las curvas abundan. El clima no es lineal. Si el viento sopla más fuerte en una dirección, puede causar más problemas en dicha dirección; puede incluso depender de la geometría de la tierra. Normalmente ves el mercado de la bolsa descrito por ecuaciones lineales y líneas rectas, pero eso no es realmente correcto. El mercado de la bolsa fluctúa arriba y abajo de modo no lineal. La ecuación de Einstein describía la curvatura del universo, y era no lineal. Terminé aprendiendo ecuaciones no lineales de un maestro, aunque no sabía que era un maestro por aquel entonces. Su nombre era Charles Morrey, y era un clásico caballero. Siempre vestía traje en clase. Era un hombre muy agradable. Incluso si yo era el único alumno, me daría clase como si lo hiciera para una clase completa.
www.cienciakanija.com
Shing-Tung Yau, chino, descubrió las dimensiones ocultas de la teoría de las cuerdas
Durante nueve meses del año, el Dr. Yau es una de Harvard profesor de matemáticas, más conocido por la invención de las estructuras matemáticas conocidas como espacios de Calabi-Yau que subyacen a la teoría de cuerdas, la supuesta "teoría del todo". En 1982 ganó una medalla de los campos, la matemática equivalente a un Premio Nobel . El Dr. Yau se puede encontrar su corte en el restaurante Yenching en Harvard Square o fuera de la biblioteca matemática en su pequeña oficina, donde la pizarra se cubre con las ecuaciones y los bocetos de rosquillas ingeniosamente troceadas.
ResponderEliminarPero los otros tres meses que es lo que su amigo Andrew Strominger, físico de la Universidad de Harvard, llamado "el ascendente emperador de la ciencia china," uno de los más destacados de los "chinos de ultramar" que vuelven a casa cada verano para trabajar, enseñar, vestíbulo, inspirar y feudo como señores de la guerra, en un esfuerzo para avanzar en la ciencia de clase mundial en china.
David J. Gross, el físico y teórico de cuerdas Nobel que dirige el Instituto Kavli de Física Teórica en Santa Bárbara, llamó al Dr. Yau "una figura de transición, entre el emperador y el demócrata."
la historia del Dr. Yau es una ventana a la dinámica que prevalecen en China 5.000 años de tradición del Reino Medio trata de mezclar con la ciencia postmoderna, una mezcla que, si se lleva, eventualmente podría formar de nuevo el equilibrio de la ciencia y la tecnología en el mundo.
"En China es una estrella de cine", dijo Ronnie Chan, un promotor inmobiliario Hong Kong y un viejo amigo que ayudó a financiar el Centro de Morningside. Y el verano pasado el Dr. Yau hizo el papel, corriendo en los coches negros de estudios de televisión a VIP recepciones en jardines prohibidos en la Ciudad Prohibida. Se hizo pasar Stephen Hawking en el Gran Salón del Pueblo en la plaza de Tiananmen para dar inicio a una reunión de algunos de los principales físicos del mundo en la teoría de cuerdas, y las vigas como un poema que había escrito fue realizado por un profesor de música en el escenario de la conferencia. Se dice en parte: "Hermosa hecho / es la fuente de truth./To medir los cambios de tiempo y espacio / los más inteligentes no son nada."
El Dr. Yau no compra el bit emperador. Cuando, protestó recientemente, es su imperio si no ejerce ninguna posición política y dos de sus estudiantes más brillantes recientes están actualmente sin empleo? "Es sólo una percepción en la medida de lo que puedo decir", dijo.
Ciertamente, su vida no es todo color de rosas. En el último año solo Dr. Yau ha participado en una pelea muy pública con la Universidad de Pekín, después de haber acusado de corrupción, y un artículo de la revista New Yorker lo retratado como un intento de entrometerse en el crédito para la solución de la conjetura de Poincaré, un famoso 100 años de edad, problema sobre la estructura del espacio.
Todo el mundo está de acuerdo en que el Dr. Yau es uno de los grandes matemáticos de la época.
"Yau realmente es un genio", dijo Robert Greene, un matemático de la Universidad de California , Los Angeles. "La cantidad y calidad de los cálculos que ha hecho es abrumador."
Pero incluso sus admiradores dicen que tiene un punto de vista político. "A medida que el sucesor de Shiing-Shen Chern como emperador de las matemáticas chinas", Deane Yang, un profesor de matemáticas en la Universidad Politécnica de Brooklyn y un viejo amigo de la familia, escribió en una carta a The New Yorker, "Yau tiene un ego descomunal y gran ambición , y ha hecho cosas que decepción de todos sus compañeros. (...) www.nytimes.com-2006
Jules Henri Poincaré nació, Francia, 29 de abril de 1854 y falleció en París, 17 de julio de 1912, generalmente conocido como Henri Poincaré (foto) , fue un prestigioso matemático, científico teórico y filósofo de la ciencia, creador de la Topología, es decir el estudio de las formas de las variedades, concepto moderno introducido a comienzos de siglo y que ha experimentado un desarrollo espectacular hasta nuestros días.
ResponderEliminarLa topología geométrica, una rama de las matemáticas que mide y establece las superficies del universo. Si bien el planteo es difícil de entender para los no especialistas, se puede decir básicamente que intenta demostrar que la esfera tridimensional es el único espacio limitado de tres dimensiones sin orificios.
La conjetura de Poincaré es una de las mayores preguntas de la topología. Las posibles aplicaciones de sus estudios van desde la industria aeroespacial a la nanotecnología ya hasta preguntas fundamentales sobre cómo funciona la naturaleza y el universo, ayuda a entender el Big Bang.
Pero ni el propio Poincaré ni nadie había podido corroborarlo hasta ahora, y por eso sigue siendo una “conjetura” y no es un “teorema”, por lo cual se constituyó en unos de los siete problemas del milenio.
En el año 2002 un matemático ruso casi desconocido, y de una personalidad reservada con muy bajo nivel de exposición publica, sorprende a la comunidad científica publicando en Internet una solución a este singular problema que había dado tanto dolores de cabeza a cientos de matemáticos de todo el mundo. Este enigmático señor, se llama Grigori Perelman, nacido un 13 de junio en Leningrado (Rusia), y a aportado novedosas soluciones a diversos problemas de topología geométrica y riemanniana.
Amante de las ciencias exactas desde su infancia y ganador de varias olimpiadas organizadas en sus país (algunas con la máxima puntuación), actualmente trabaja en Instituto Steklov de Matemáticas de la Academia Rusa de las Ciencias.
En 2006 dos matemáticos chinos, apoyándose en los estudios del estadounidense Richard Hamilton, publicaron otra solución (aparentemente mejor) afirmando que era una demostración completa de las conjeturas de Poincaré y geometrización, y desde aquel instante la comunidad matemática se dividió respecto a quien tenía razón. Estos matemáticos orientales aducían que Perelman solo había planteado una demostración en líneas generales y no expresó con rigurosos argumentos matemáticos como se resolvía el enigma matemático, dejando “huecos” absurdos. (parece que esos huecos fue debido a la forma informal en que presentó inicialmente la solución).
La demostración le llevó 8 años de trabajo, y llenó un cuaderno de mas de 470 páginas, y por dicha demostración fue premiado por diversas instituciones y academias mundiales, pero él no acepta el dinero otorgado.
Rechazó la Medalla Fields (una especie de Nobel de las Matemáticas, dotado con 10.000 dólares) entregada por el Rey Juan Carlos I de España
Vive en San Petersburgo, en un sencillo apartamento, junto a su anciana madre. Se mantiene dando clases particulares, viviendo muy austeramente.
historiasybiografias.com